Определение. Матрицу В называют транспонированной матрицей А, а переход от А к В транспонированием, если элементы каждой строки матрицы А записать в том же порядке в столбцы матрицы В.

А = ;                    В = А^Т=;

 

другими словами,  b_ji = a_ij.

 

            В качестве следствия из предыдущего свойства (5) можно записать, что:

(ABC)^T = C^TB^TA^T,

при условии, что определено произведение матриц АВС.

5) Если определено произведение АВ , то определено произведение В^ТА^Т и выполняется равенство:

(АВ)^Т = В^ТА^Т, где

индексом Т обозначается транспонированная матрица.

Пример.    Даны матрицы А = , В = , С =  и число a = 2. Найти А^ТВ+aС.

            A^T = ;                 A^TB = × =  = ;

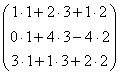aC = ;                           А^ТВ+aС = + = .

 

            Пример. Найти произведение матриц А =  и В = .

АВ = × = .

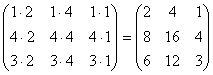ВА = × = 2×1 + 4×4 + 1×3 = 2 + 16 + 3 = 21.

            Пример. Найти произведение матриц А=, В =

АВ = ×= = .