Матричный метод решения систем линейных уравнений.

 

 

            Матричный метод применим к решению систем уравнений, где число уравнений равно числу неизвестных.

            Метод удобен для решения систем невысокого порядка.

            Метод основан на применении свойств умножения матриц.

 

            Пусть дана система уравнений: 

Составим матрицы:   A = ;             B = ;           X = .

 

Систему уравнений можно записать:

A×X = B.

 

Сделаем следующее преобразование: A^-1×A×X = A^-1×B,

 

т.к.   А^-1×А = Е, то  Е×Х = А^-1×В

Х = А^-1×В

            Для применения данного метода необходимо находить обратную матрицу, что может быть связано с вычислительными трудностями при решении систем высокого порядка.

 

            Пример. Решить систему уравнений:

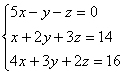
Х = , B = , A =

Найдем обратную матрицу А^-1.

D = det A = 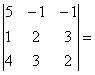5(4-9) + 1(2 – 12) – 1(3 – 8) = -25 – 10 +5 = -30.

 

M₁₁ =  = -5;                  M₂₁ =  = 1;                   M₃₁ =    = -1;

M₁₂ =                M₂₂ =                     M₃₂ =

M₁₃ =                  M₂₃ =                     M₃₃ =

 

 

                     A^-1 = ;

 

Cделаем проверку:

A×A^-1 = =E.

 

Находим матрицу Х.

Х = = А^-1В = ×= .

 

Итого решения системы: x =1; y = 2; z = 3.