Расстояние от точки до плоскости.

 

            Расстояние от произвольной точки М₀(х₀, у₀, z₀)  до плоскости Ах+Ву+Сz+D=0 равно:

 

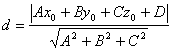
            Пример. Найти уравнение плоскости, зная, что точка Р(4; -3; 12) – основание перпендикуляра, опущенного из начала координат на эту плоскость.

 

           

 

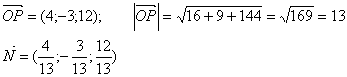
Таким образом, A = 4/13;  B = -3/13;   C = 12/13, воспользуемся формулой:

 

A(x – x₀) + B(y – y₀) + C(z – z₀) = 0.

 

 

 

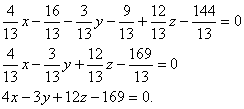
            Пример. Найти уравнение плоскости, проходящей через две точки P(2; 0; -1) и

Q(1; -1; 3)  перпендикулярно плоскости 3х + 2у – z + 5 = 0.

 

            Вектор нормали к плоскости 3х + 2у – z + 5 = 0 параллелен искомой плоскости.

            Получаем:

 

 

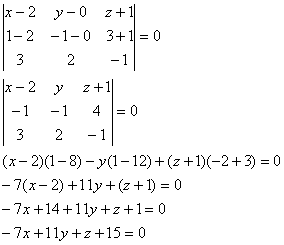
            Пример. Найти уравнение плоскости, проходящей через точки А(2, -1, 4) и

В(3, 2, -1) перпендикулярно плоскости х + у + 2z – 3 = 0.

 

            Искомое уравнение плоскости имеет вид: Ax + By + Cz + D = 0, вектор нормали к этой плоскости (A, B, C). Вектор (1, 3, -5) принадлежит плоскости. Заданная нам плоскость, перпендикулярная искомой имеет вектор нормали (1, 1, 2). Т.к. точки А и В принадлежат обеим плоскостям, а плоскости взаимно перпендикулярны, то

            Таким образом, вектор нормали (11, -7, -2). Т.к. точка А принадлежит искомой плоскости, то ее координаты должны удовлетворять уравнению этой плоскости, т.е. 11×2 + 7×1 - 2×4 + D = 0;    D = -21.

 

                Итого, получаем уравнение плоскости: 11x - 7y – 2z – 21 = 0.

 

 

            Пример. Найти уравнение плоскости, зная, что точка Р(4, -3, 12) – основание перпендикуляра, опущенного из начала координат на эту плоскость.

 

            Находим координаты вектора нормали = (4,  -3, 12). Искомое уравнение плоскости имеет вид: 4x – 3y + 12z + D = 0. Для нахождения коэффициента D подставим в уравнение координаты точки Р:

16 + 9 + 144 + D = 0

D = -169

            Итого, получаем искомое уравнение: 4x – 3y + 12z – 169 = 0

 

 

Пример. Даны координаты вершин пирамиды А₁(1; 0; 3), A₂(2; -1; 3), A₃(2; 1; 1),

A₄(1; 2; 5).

 

1)      Найти длину ребра А₁А₂.

 

2)      Найти угол между ребрами А₁А₂ и А₁А₄.

           

3)      Найти угол между ребром А₁А₄ и гранью А₁А₂А₃.

 

Сначала найдем вектор нормали к грани А₁А₂А₃  как векторное произведение векторов и.

 

= (2-1; 1-0; 1-3) = (1; 1; -2);

 

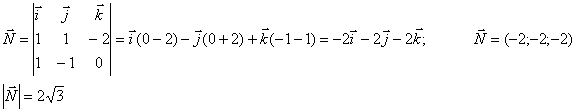
            Найдем угол между вектором нормали и вектором .

-4 – 4 = -8.

Искомый угол g между вектором и плоскостью будет равен g = 90⁰ - b.

 

4)      Найти площадь грани А₁А₂А₃.

 

 

5)      Найти объем пирамиды.

 

 (ед³).

 

6)      Найти уравнение плоскости А₁А₂А₃.

 

Воспользуемся формулой уравнения плоскости, проходящей через три точки.

 

2x + 2y + 2z – 8 = 0

 

x + y + z – 4 = 0;

 

 

 

            При использовании компьютерной версии “Курса высшей математики” можно запустить программу, которая решит рассмотренный выше пример для любых координат вершин пирамиды.

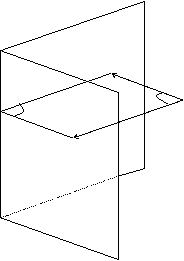
Угол между плоскостями.

 

 

 

 

 

                                                                                        

                                                                                                j₁

                                                           j                                   0

                                                                                  

 

 

 

 

 

 

            Угол между двумя плоскостями в пространстве j связан с углом между нормалями к этим плоскостям j₁ соотношением: j = j₁ или j = 180⁰ - j₁, т.е.

cosj = ±cosj₁.

            Определим угол j₁. Известно, что плоскости могут быть заданы соотношениями:

, где

(A₁, B₁, C₁), (A₂, B₂, C₂). Угол между векторами нормали найдем из их скалярного произведения:

.

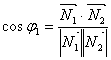            Таким образом, угол между плоскостями находится по формуле:

 

 

            Выбор знака косинуса зависит от того, какой угол между плоскостями следует найти – острый, или смежный с ним тупой.

 

Условия параллельности и перпендикулярности

плоскостей.

 

            На основе полученной выше формулы для нахождения угла между плоскостями можно найти условия параллельности и перпендикулярности плоскостей.

           

            Для того, чтобы плоскости были перпендикулярны необходимо и достаточно, чтобы косинус угла между плоскостями равнялся нулю. Это условие выполняется, если:

.

 

            Плоскости параллельны, векторы нормалей коллинеарны: ïï.Это условие выполняется, если: .