Криволинейные интегралы второго рода.

 

            Пусть АВ – непрерывная кривая в пространстве XYZ (или на плоскости ХОY), а точка P(x, y, z) – произвольная функция, определенная на этой кривой. Разобьем кривую точками  на конечное число частичных дуг. И рассмотрим сумму произведений значений функции в каждой точке на длину соответствующей частичной дуги.

 ;  

 

            Определение. Если при стремлении к нулю шага разбиения кривой АВ интегральные суммы имеют конечный предел, то этот предел называется криволинейным интегралом по переменной х от функции P(x, y, z) по кривой АВ в направлении от А к В.

 

            Криволинейный интеграл второго рода, т.е. интеграл по координатам отличается от криволинейного интеграла первого рода, т.е. по длине дуги тем, что значение функции при составлении интегральной суммы умножается не на длину частичной дуги, а на ее проекцию на соответствующюю ось. (В рассмотренном выше случае – на ось ОХ).

            Вообще говоря, криволинейные интегралы могут считаться также и по переменным у и z.

 

            Сумму криволинейных интегралов также называют криволинейным интегралом второго рода.

 

Свойства криволинейного интеграла второго рода.

 

            1) Криволинейный интеграл при перемене направления кривой меняет знак.

 

            2) 

 

            3)

 

            4)

 

            5) Криволинейный интеграл по замкнутой кривой L не зависит от выбора начальной точки, а зависит только от направления обхода кривой.

            Направление обхода контура L задается дополнительно. Если L – замкнутая кривая без точек самопересечения, то направление обхода контура против часовой стрелки называется положительным.

 

            6) Если АВ – кривая, лежащая в плоскости, перпендикулярной оси ОХ, то

Аналогичные соотношения справедливы при интегрировании по переменным у и z.

 

            Теорема. Если кривая АВ – кусочно- гладкая, а функции P(x, y, z), Q(x, y, z) и

R(x, y, z) – непрерывны на кривой АВ, то криволинейные интегралы

существуют.

 

            Вычисление криволинейных интегралов второго рода производится путем преобразования их к определенным интегралам по формулам:

           

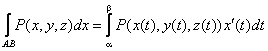
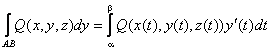
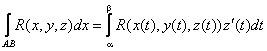
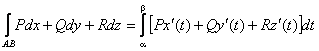
В случае, если АВ – плоская кривая, заданная уравнением y = f(x), то

 

 

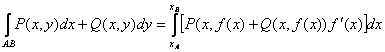
            Пример. Вычислить криволинейный интеграл . L – контур, ограниченный параболами . Направление обхода контура положительное.

 

 

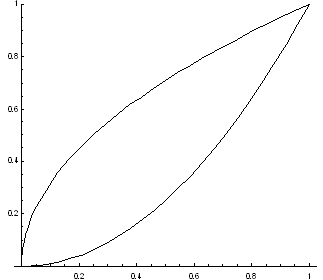
            Представим замкнутый контур L как сумму двух дуг L₁ = x² и