Молекулярно-кинетическая теория
идеального газа
Уравнение состояния
идеального газа в термодинамике получают как обобщение опытных фактов. В
молекулярно-кинетической теории его можно вывести, пользуясь законами
механики. В качестве модели идеального газа при этом выбирают систему твердых
упругих шариков очень малого размера, энергией взаимодействия между которыми
можно пренебречь и которые движутся совершенно хаотически.
Если такой шарик ударяется
о стенку, как изображенона рисунке, изменение его импульса равно  . За
время . За
время  до
стенки долетят молекулы, удаленные на расстояние до
стенки долетят молекулы, удаленные на расстояние  ; если
число молекул в единице объема равно n, число ударово стенку за время ; если
число молекул в единице объема равно n, число ударово стенку за время  : :

где S - площадь стенки.
Множитель  появился в следствии
того, что из-за хаотичности движения молекул половина их будет иметь скорость появился в следствии
того, что из-за хаотичности движения молекул половина их будет иметь скорость
 , направленную к
стенке, а другая половина - от стенки. , направленную к
стенке, а другая половина - от стенки.
Импульс средней силы,
действующей на стенку со стороны всех молекул, по 2-му закону Ньютона равен:

(черточка сверху означает
усреднение по всем молекулам газа). Давление газа на стенку равно  . Так как все
направления движения равновероятны, . Так как все
направления движения равновероятны,  . Итак, . Итак, 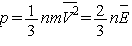 , где , где 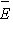 -
средняя кинетическая энергия молекул газа. -
средняя кинетическая энергия молекул газа.
Если в сосуде заключен
один моль газа, а объем сосуда равен V, 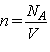 , и мы получаем , и мы получаем 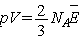 ( ( 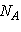 - число Авогадро).
Сравним эту формулу с уравнением состояния идеального газа, полученным в
термодинамике: - число Авогадро).
Сравним эту формулу с уравнением состояния идеального газа, полученным в
термодинамике: 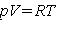 . Эти два уравнения
совпадают, если . Эти два уравнения
совпадают, если 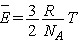 . Коэффициент . Коэффициент 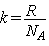 -
постоянная Больцмана, -
постоянная Больцмана, 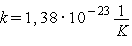 . Это очень важная
физическая константа, следует ее запомнить. Итак, . Это очень важная
физическая константа, следует ее запомнить. Итак,
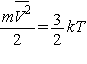 , а , а 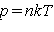
Итак, на модели идеального
газа мы показали, что температура с точки зрения молекулярно-кинетической
теории определяется (с точностью до коэффициента, связанного с выбором
системы единиц) средней кинетической энергией молекул. При этом
среднеквадратичная скорость молекул газа зависит лишь от температуры и массы
молекул (или молярной массы): 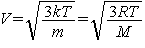 , где М - молярная
масса газа. Энергия, приходящаяся при этом на движение вдоль какой-либо
выбранной оси (как принято говорить, "энергия, приходящаяся на одну
степень свободы") , где М - молярная
масса газа. Энергия, приходящаяся при этом на движение вдоль какой-либо
выбранной оси (как принято говорить, "энергия, приходящаяся на одну
степень свободы") 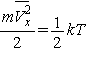 . Напомним, что все
приведенные выше формулы получены для модели газа, состоящего из очень
маленьких шариков. Эта модель хорошо подходит для одноатомного газа. Такой
атом может обладать только запасом кинетической энергии поступательного
движения. Молекулы двух- и многоатомных газов имеют более сложное строение:
ведь масса атома сосредоточена, в основном, в ядре, имеющем размеры . Напомним, что все
приведенные выше формулы получены для модели газа, состоящего из очень
маленьких шариков. Эта модель хорошо подходит для одноатомного газа. Такой
атом может обладать только запасом кинетической энергии поступательного
движения. Молекулы двух- и многоатомных газов имеют более сложное строение:
ведь масса атома сосредоточена, в основном, в ядре, имеющем размеры 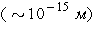 много меньшие, чем много меньшие, чем
расстояния между ядрами в
молекуле (порядка размера атома, т. е. 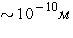 ). Поэтому молекулу
двухатомного газа можно представить себе как гантель, состоящую из двух
шариков размером ). Поэтому молекулу
двухатомного газа можно представить себе как гантель, состоящую из двух
шариков размером 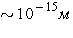 , отстоящих друг от
друга на расстояние , отстоящих друг от
друга на расстояние 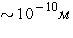 (см. рис. 2 ). Такая
система, кроме энергии поступательного движения, обладает еще и запасом
энергии вращательного движения по осям х и z (вращением вокруг оси Оу можно
пренебречь, т. к. (см. рис. 2 ). Такая
система, кроме энергии поступательного движения, обладает еще и запасом
энергии вращательного движения по осям х и z (вращением вокруг оси Оу можно
пренебречь, т. к. 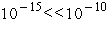 ). ).
Оказывается, что в
классической (не квантовой) физике можно считать, что средняя кинетическая
энергия, приходящаяся при тепловом равновесии на одну степень свободы
любой атомно-молекулярной системы, равна 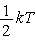 . .
Таким образом, полный
запас энергии у любой двухатомной молекулы при температуре Т (независимо от
сорта газа) будет 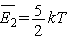 . У трехатомных газов
(и любых других многоатомных газов) вращательная энергия приходится на все
три возможных независимых оси вращения (х, у, z) и, следовательно, молекула
любого многоатомного газа при температуре Т имеет энергию . У трехатомных газов
(и любых других многоатомных газов) вращательная энергия приходится на все
три возможных независимых оси вращения (х, у, z) и, следовательно, молекула
любого многоатомного газа при температуре Т имеет энергию 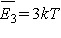 . .
|

|
|
 Содержание Содержание
|
·
Молекулярно-кинетическая
теория идеального газа
·
Пример1
·
Пример2
·
Пример3
|
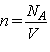 , и мы получаем
, и мы получаем 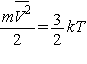 , а
, а 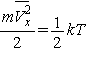 . Напомним, что все
приведенные выше формулы получены для модели газа, состоящего из очень
маленьких шариков. Эта модель хорошо подходит для одноатомного газа. Такой
атом может обладать только запасом кинетической энергии поступательного
движения. Молекулы двух- и многоатомных газов имеют более сложное строение:
ведь масса атома сосредоточена, в основном, в ядре, имеющем размеры
. Напомним, что все
приведенные выше формулы получены для модели газа, состоящего из очень
маленьких шариков. Эта модель хорошо подходит для одноатомного газа. Такой
атом может обладать только запасом кинетической энергии поступательного
движения. Молекулы двух- и многоатомных газов имеют более сложное строение:
ведь масса атома сосредоточена, в основном, в ядре, имеющем размеры