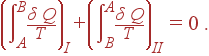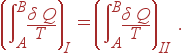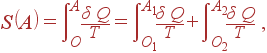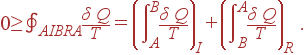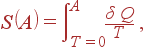Энтропия

Уравнение Клаузиуса (31) можно обобщить на случай, когда система, совершающая циклический процесс, обменивается теплотой не с двумя, а с n источниками, имеющими температуры T₁,T₂,...,T_n. В этом случае (31) заменяется на уравнение

$\sum\limits_{i=1}^n\frac{\Delta Q_i}{T_i}=0 ,$

(34)

где Δ Q_i – количество теплоты, получаемое системой от i-го источника. В случае же, когда система обменивается теплотой с непрерывно распределенными источниками, сумма по n заменяется интегралом, взятым по всему циклу, и уравнение Клаузиуса принимает вид

$\oint \frac{\delta Q}T=0 .$

(35)

Уравнение Клаузиуса справедливо, если все части цикла представляют собой обратимые процессы и цикл является обратимым. Если же цикл включает в себя необратимый процесс и оказывается необратимым, то уравнение (35) не выполняется и имеет место неравенство Клаузиуса

$\oint \frac{\delta Q}T<0 .$

(36)

Свойство обратимых циклов, выражаемое уравнением Клаузиуса (35), можно представить в иной форме. Рассмотрим обратимый процесс, при котором система переходит из состояния A в состояние B. Обычно возможно множество различных обратимых процессов, переводящих систему из одного равновесного состояния в другое. Любой непрерывной кривой, соединяющей точки A и B на диаграмме (V,P), соответствует возможный обратимый процесс от A до B.

На рис. 1.4 показаны два таких процесса. Рассмотрим цикл AIBIIA, составленный из двух произвольных обратимых процессов I и II, соединяющих точки A и B на рис. 1.4. Поскольку этот цикл является обратимым, то согласно (35)

$\oint_{AIBIIA}\frac{\delta Q}T=0 .$

(37)

Разобьем интеграл по циклу на сумму двух интегралов, первый из которых берется по пути AIB, а второй – по пути BIIA, т.е. перепишем (37) в форме

$\left( \int\limits_A^B\frac{\delta Q}T\right) _I+\left( \int\limits_B^A\frac{\delta Q}T\right) _{II}=0 .$

Если перенести теперь второй интеграл направо и поменять в нем пределы интегрирования, то получается соотношение

$\left( \int\limits_A^B\frac{\delta Q}T\right) _I=\left( \int\limits_A^B\frac{\delta Q}T\right) _{II} .$

Таким образом, интеграл

$\int\limits_A^B\frac{\delta Q}T$

зависит только от начального и конечного состояний A и B, но не зависит от самого процесса, т.е. является одним и тем же для всех обратимых процессов от A до B.

Это свойство позволяет ввести новую функцию состояния системы, называемую энтропией, которая представляет собой исключительно важную термодинамическую величину. Энтропией состояния A называется величина

$S\left( A\right) =\int\limits_O^A\frac{\delta Q}T ,$

(38)

где интеграл берется по произвольному обратимому процессу от состояния O, прнятого за начало отсчета.

Определим разность энтропий в состояниях A и B. Для этого рассмотрим обратимый цикл OBAO. Поскольку цикл обратим, то интеграл

$\oint_{OBAO}\frac{\delta Q}T=0 .$

Разобьем интеграл по циклу на сумму трех интегралов:

$\int\limits_O^B\frac{\delta Q}T+\int\limits_B^A\frac{\delta Q}T+ \int\limits_A^O\frac{\delta Q}T=0 .$

Согласно определению (38) первый интеграл представляет энтропию в состоянии B, а третий – энтропию в состоянии A со знаком минус. Отсюда следует, что

$S\left( B\right) -S\left( A\right) =\int\limits_A^B\frac{\delta Q}T ,$

(39)

где интеграл берется по произвольному обратимому процессу от A до B.

Формула (38) представляет энтропию с точностью до аддитивной постоянной. Эта неопределенность не проявляется, если нас интересует разность энтропии в различных состояниях (39), которая не зависит от состояния O, принятого за начало отсчета. Однако в некоторых случаях аддитивная константа играет важную роль. Величина ее устанавливается третьим законом термодинамики, о котором речь будет позже.

Если от конечного процесса перейти к бесконечно малому процессу, то (39) принимает вид

$dS=\frac{\delta Q}T ,$

(40)

т.е. изменение энтропии при бесконечно малом обратимом процессе равно количеству теплоты δ Q, деленному на температуру системы T.

Формула (40) означает, что отношение δ Q/T является полным дифференциалом, в то время как δ Q не является таковым. Это соотношение представляет следствие постулата Клаузиуса. Поэтому его часто называют вторым законом термодинамики, математическим следствием которого оно и является.

Подставим сооотношение δ Q = TdS в уравнение первого закона термодинамики (9). В результате получаем дифференциальное уравнение

dE = TdS–PdV ,

(41)

которое называется основным термодинамическим тождеством. Оно объединяет первый и второй законы термодинамики и справедливо для бесконечно малых обратимых процессов.

Энтропия составной системы равна сумме энтропий ее частей. Это верно, если энергия и работа аддитивны, т.е. если энергия системы равна сумме энергий всех ее частей, а работа, совершаемая системой, равна сумме работ, совершаемых ее частями. Энергия системы аддитивна, если можно пренебречь энергией взаимодействия подсистем по сравнению с их энергиями, т.е. если поверхностная энергия мала по сравнению с объемной. Для системы, состоящей из двух различных веществ, это так, если они не очень сильно размельчены. В противном случае поверхностная энергия играет важную роль.

Итак, если система состоит из двух частей и внутренняя энергия и работа аддитивны,

E = E₁+E₂ , L = L₁+L₂ ,

то поглощаемая системой теплота также аддитивна: Q = Q₁+Q₂. Это означает, что аддитивна и энтропия:

$S\left( A\right) =\int\limits_O^A\frac{\delta Q}T=\int\limits_{O_1}^{A_1}\frac{\delta Q}T+\int\limits_{O_2}^{A_2}\frac{\delta Q}T ,$

(42)

где O_1,2 и A_1,2 обозначают состояния подсистем, когда составная система находится в состояниях O и A соответственно.

Отметим, что выражение (42) можно использовать для определения энтропии системы, не находящейся в состоянии равновесия, если ее можно разбить на части, находящиеся в равновесных состояниях.

Изменение энтропии системы при переходе из состояния A в B определяется уравнением (39), если интеграл берется по обратимому процессу. Если же интеграл берется по необратимому процессу, то равенство (39) нарушается. Чтобы определить изменение энтропии в этом случае, рассмотрим необратимый цикл AIBRA, состоящий из необратимого процесса I от A до B и обратимого процесса R от B до A (рис. 1.5).

Применяя неравенство Клаузиуса (36) к этому циклу, имеем

$0\geq \oint_{AIBRA}\frac{\delta Q}T=\left( \int\limits_A^B\frac{\delta Q}T\right) _I+\left( \int\limits_B^A\frac{\delta Q}T\right) _R .$

(43)

К обратимому процессу R можно применить соотношение (39), согласно которому второе слагаемое в (43) равно разности $S\left( A\right) -S\left( B\right) .$ Это приводит к неравенству

$S\left( B\right) -S\left( A\right) \geq \int\limits_A^B\frac{\delta Q}T,$

(44)

где интеграл берется по произвольному необратимому процессу I от A до B.

Закон возрастания энтропии

Применим неравенство (44) к изолированной системе, которая никак не взаимодействует с окружающей средой. Поскольку для такой системы δ Q = 0, то (44) принимает вид:

$S\left( B\right) \geq S\left( A\right) ,$

(45)

т.е. для любого процесса в изолированной системе энтропия конечного состояния не может быть меньше энтрпии начального состояния. Это – закон возрастания энтропии.

Если процесс обратим, то в (45) стоит знак равенства, т.е. энтропия системы не меняется.

Закон возрастания энтропии справедлив только для изолированных систем. С помощью внешней системы можно уменьшить энтропию тела. Однако суммарная энтропия тела и внешней системы уменьшиться не может.

Если изолированная система находится в состоянии с максимальной энтропией, сооответствующей ее энергии, то в ней не могут происходить никакие процессы, поскольку любой процесс привел бы к уменьшению энтропии. Таким образом, состояние с максимальной энтропией является наиболее устойчивым состоянием изолированной системы.

Самопроизвольные процессы в изолированных системах идут в направлении роста энтропии. Продемонстрируем это двумя примерами.

1. Рассмотрим теплообмен между двумя частями системы A₁ и A₂, имеющими температуры T₁ и T₂. Пусть T₁<T₂. Теплота передается от горячего тела к холодному. Поэтому тело A₂ передаст телу A₁ некоторое количество теплоты Q, т.е.

Δ Q₁ = Q , Δ Q₂ = –Q .

При этом энтропия тела A₁ изменится на величину Δ Q₁/T₁ , а энтропия тела A₂ – на величину Δ Q₂/T₂ . Общее изменение энтропии системы

$\Delta S=\frac{\Delta Q_1}{T_1}+\frac{\Delta Q_2}{T_2}=Q\left( \frac 1{T_1}-\frac 1{T_2}\right) .$

(46)

Поскольку T₁<T₂ , то Δ S>0 .

2. Рассмотрим теперь выделение теплоты при трении. Энтропия тела, которое нагревается при трении, возрастает. Это увеличение энтропии не компенсируется уменьшением энтропии других частей системы, так как теплота получена из работы.

Энтропия равновесных систем

Рассмотрим систему, состояние которой в равновесии определяется какими-либо двумя из трех переменных P, V и T. Возьмем в качестве независимых переменных T и V. Тогда теплота δ Q, получаемая системой при обратимом процессе, при котором T и V изменяются на dT и dV, определяется выражением (13). Соответствующее изменение энтропии

$dS=\frac{\delta Q}T=\frac 1T\left( \frac{\partial E}{\partial T}\right)_VdT+ \frac 1T\left[ \left( \frac{\partial E}{\partial V}\right) _T+P\right]dV .$

(47)

Важное отличие (47) от (13) состоит в том, что dS – полный дифференциал, а δ Q – нет. Это следует из того, что S - функция состояния системы, изменение которой зависит только от начального и конечного состояний, но не от самого процесса. Так, изменения энтропии для двух различных процессов I и II, переводящих систему из состояния A в состояние B (см. рис. 4), равны $S\left( A\right) -S\left( B\right)$ и, следовательно, одинаковы. В противоположность этому не существует функции состояния $Q\left( T, V\right)$ , полным дифференциалом которой была бы правая часть (13). Действительно, количество теплоты Q_I, полученное системой во время процесса I, отличается от Q_II. Это следует из первого закона термодинамики (7), применение которого к процессам I и II дает

Q_I = E_B–E_A+L_I, Q_II = E_B–E_A+L_II ,

(48)

где L_I и L_II определяются площадями под кривыми I и II соответственно. Беря разность Q_I–Q_II , получаем

Q_I–Q_II = L_I–L_II .

(49)

Но разность L_I–L_II равна площади между кривыми I и II. Следовательно, Q_I и Q_II различаются. Таким образом, количество теплоты, полученное системой во время процесса, зависит не только от начального и конечного состояний, но и от самого процесса. Другими словами, не существует функции $Q\left( T,V\right)$ и, следовательно, δ Q не является полным дифференциалом.

Поскольку dS - полный дифференциал, то его можно представить в виде

$dS=\left( \frac{\partial S}{\partial T}\right) _VdT+\left( \frac{\partial S}{\partial V}\right) _TdV .$

Сравнение этого выражения с (47) дает уравнения

$\left( \frac{\partial S}{\partial T}\right) _V=\frac 1T\left( \frac{\partial E}{\partial T}\right) _V , \left( \frac{\partial S}{\partial V}\right) _T=\frac 1T\left[ \left( \frac{\partial E}{\partial V}\right) _T+P\right] .$

(50)

Если первое уравнение продифференцировать по V, а второе – по T, то слева получается одна и та же величина ∂ ²S/∂ T∂ V. Следовательно, равны и производные от правых частей уравнений (50), т.е.

$\frac 1T\frac{\partial ^2E}{\partial V\partial T}=\frac \partial {\partial T}\left( \frac 1T\left[ \left( \frac{\partial E}{\partial V}\right) _T+P\right] \right) _V .$

(51)

Производя дифференцирование по T в правой части (51), получаем

$\frac 1T\frac{\partial ^2E}{\partial V\partial T}=\frac 1T\frac{\partial ^2E}{\partial V\partial T}-\frac 1{T^2}\left( \frac{\partial E}{\partial V}\right) _T+\frac \partial {\partial T}\left( \frac PT\right) _V ,$

откуда

$\left( \frac{\partial E}{\partial V}\right) _T=T^2\frac \partial {\partial T}\left( \frac PT\right) _V .$

(52)

Это – важное соотношение, которое часто используется при решении термодинамических задач. В частности, с его помощью можно показать, что внутренняя энергия идеального газа не зависит от объема. Действительно, используя уравнение состояния идеального газа (3), имеем

$\frac \partial {\partial T}\left( \frac PT\right) _V=\frac \partial {\partial T}\left( \frac{NR}V\right) _V=0 ,$

(53)

так что (52) дает

$\left( \frac{\partial E}{\partial V}\right) _T=0 ,$

т.е. внутренняя энергия идеального газа зависит только от температуры:

$E=E\left( T\right) .$

(54)

Выражение для частной производной (∂ E/∂ V)_T можно записать иначе, если в правой стороне (52) продифференцировать по T. Тогда

$\left( \frac{\partial E}{\partial V}\right) _T=T\left( \frac{\partial P}{\partial T}\right) _V-P.$

Подставляя это выражение в формулу (47) для dS, получаем

$d S=\frac 1T\left( \frac{\partial E}{\partial T}\right) _VdT+\left( \frac{\partial P}{\partial T}\right) _V dV .$

(55)

В качестве примера вычислим энтропию одного моля идеального газа. Принимая во внимание, что $\left( \partial \widetilde{E}/\partial T\right) _V=C_V$ и выражая давление P через T и $\widetilde{V}$ из уравнения состояния, преобразуем (55) к виду

$d \widetilde{S}=C_V \frac{d T}T+R\frac{ d\widetilde{V}}{ \widetilde{V }} .$

(56)

Это выражение удовлетворяет основному требованию, предъявляемому к полным дифференциалам, а именно: перекрестные производные от функций, на которые умножаются dT и $d\widetilde{V} ,$ равны друг другу. Интегрируя (56), находим

$\widetilde{S}=C_V \ln T+R \ln \widetilde{V}+S_0 ,$

(57)

где S₀ - константа интегрирования.

Иначе обстоит дело с выражением для элементарной теплоты

$\delta \widetilde{Q}=C_VdT+P d\widetilde{V}=C_VdT+\frac{RT}{\widetilde{V}} d\widetilde{V} .$

(58)

В этом случае перекрестные производные не равны друг другу. Поэтому функции T и $\widetilde{V} ,$ полным дифференциалом которой было бы это выражение, не существует.

В заключение сформулируем общий критерий, который позволяет заключить, является ли то или иное выражение полным дифференциалом. Дифференциальная форма

M(x,y)dx+N(x,y)dy

(59)

является полным дифференциалом некоторой функции F(x,y) при условии равенства перекрестных производных от M и N:

$\frac{\partial M(x,y)}{\partial y}=\frac{\partial N(x,y)}{\partial x} .$

(60)

Докажем это. Полный дифференциал dF можно представить в форме

$dF(x,y)=\frac{\partial F(x,y)}{\partial x} dx+\frac{\partial F(x,y)}{\partial y} dy .$

(61)

Сравнение (59) с (61) приводит к уравнениям

$\frac{\partial F(x,y)}{\partial x}=M(x,y) , \frac{\partial F(x,y)}{\partial y}=N(x,y) .$

(62)

Дифференцируя теперь первое из этих уравнений по y, а второе – по x и учитывая, что

$\frac{\partial ^2F(x,y)}{\partial y\partial x}=\frac{\partial ^2F(x,y)}{\partial x\partial y} ,$

мы, действительно, приходим к условию (60).

Третий закон термодинамики (теорема Нернста)

В разделе 1.11 мы уже упоминали, что определение энтропии (38) не является однозначным, поскольку произвол в выборе начала отсчета O вводит в энтропию неопределенную аддитивную константу. Если рассматривается изменение энтропии (39), такой неопределенности нет. Однако в ряде случаев, как, например, при рассмотрении химических реакций знание этой константы является важным.

Значение аддитивной константы, возникающей при определении энтропии, устанавливается теоремой Нернста, которую часто называют третьим законом термодинамики: энтропия любой системы при абсолютном нуле температуры всегда может быть принята равной нулю.

Физический смысл теоремы состоит в том, что при T = 0 все возможные состояния системы имеют одинаковую энтропию. Поэтому состояние системы при T = 0 удобно взять в качестве начального состояния О и положить энтропию этого состояния равной нулю. Тогда энтропию произвольного состояния A можно определить интегралом

$S\left( A\right) =\int\limits_{T=0}^A\frac{\delta Q}T ,$

(63)

где интегрирование производится вдоль обратимого процесса, начинающегося от состояния при T = 0 и заканчивающегося состоянием A.

В термодинамике теорема Нернста принимается как постулат. Доказывается она методами квантовой статистики.

Из теоремы Нернста следует важный вывод о поведении теплоемкости тел при T→ 0. Рассмотрим нагревание твердого тела. При изменении его температуры T на dT тело поглощает количество теплоты

δ Q = C(T) dT ,

(64)

где C(T) - его теплоемкость. Поэтому согласно определению (63) энтропию тела при температуре T можно представить в форме

$S\left( T\right) =\int\limits_0^T\frac{C(T^{\prime })}{T^{\prime }}dT^{\prime } .$

(65)

Из этой формулы видно, что если бы теплоемкость тела при абсолютном нуле, C(0), отличалась от нуля, то интеграл (65) расходился бы на нижнем пределе. Поэтому при T = 0 теплоемкость должна равняться нулю:

C(0) = 0 .

(66)

Этот вывод находится в согласии с экспериментальными данными по теплоемкости тел при T→ 0 .

Следет отметить, что (66) относится не только к твердым телам, но и к газам. Сделанное ранее утверждение о том, что теплоемкость идеального газа не зависит от температуры, справедливо только для не слишком низких температур. При этом нужно иметь в виду два обстоятельства.

1. При низких температурах свойства любого газа сильно отличаются от свойств идеального газа, т.е. вблизи абсолютного нуля ни одно вещество не является идеальным газом.

2. Если бы даже идеальный газ мог существовать вблизи нуля температуры, то строгое вычисление его теплоемкости методами квантовой статистики показывает, что она стремилась бы к нулю при T→ 0 .