Общая характеристика гармонических колебаний. Метод векторных диаграмм.

Виды колебаний. Рассмотрим причины, по которым колебания рассматриваются в курсе "Механика" и выделяются в самостоятельный раздел. Они заключаются в следующем:

Среди всех колебаний особая роль отводится гармоническим ввиду следующих причин:

Колебание – повторяющийся процесс изменения некоторой физической величины около ее среднего значения.
В механических колебаниях речь идет об описании изменения во времени отклонения тела от положения равновесия.

Форма колебаний может быть разной. Выделяют непериодические, периодические и гармонические колебания (см. рис. 9.1).

Рис. 9.1. Виды колебаний.

Определение гармонических колебаний. Гармоническими называются колебания, при которых описываемая физическая величина изменяется по закону синуса или косинуса. Уравнение кинематики гармонических колебаний имеет следующий вид:

x = A·cos(2p·t/T + f₀),     (9.1)
где х - колеблющаяся величина,
t - время;
А, Т, f - константы для данного колебания, называемые параметрами. 

Гармонические колебания являются частным случаем периодических колебаний.

Параметры гармонических колебаний. Постоянные величины А, Т, f, входящие в уравнение (9.1), называются параметрами колебания. Рассмотрим их физический смысл.

Из (9.1) следует, что в случае, если соs(2p·t/Т + f) = ± 1, то  значение модуля x максимально, т.е. |x| = x_max = A. Величину А, равную наибольшему значению колеблющейся физической величины, назовем амплитудой колебания. 

В случае изменения времени на величину, кратную T, аргумент функции косинус изменится на величину, кратную 2p, а х и ее производная примут первоначальные значения:

x(t) = x(t + n·T),   u(t) = u(t + n·T)
где Т - период, минимальное время, по истечение которого процесс колебаний  полностью повторяется$
n - целое число.

Период колебаний - наименьшее время по истечении которого движение полностью повторяется, т.е. сама колеблющаяся величина и ее скорость принимают прежние значения.

Величина, обратная периоду колебаний Т, называется частотой n = 1/Т. Частота - есть число колебаний, совершаемое системой, за 1 секунду. Циклическая или круговая частота - есть число колебаний за 2p секунд w = 2p/Т = 2p·n.

Мгновенное значение физической величины х определяется значением аргумента функции косинус, который называется фазой колебаний: 

Ф = w·t + f₀.

Рис. 9.2. Зависимость фазы гармонических колебаний от времени.

Рис. 9.3.

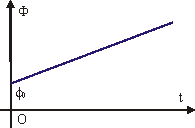
Фаза колебаний Ф линейно растет со временем (см. рис. 9.2). При t = 0 значение Ф равняется f₀, которое называется начальной фазой колебания. Начальную фазу можно рассчитать, исходя из значения физической величины в начальный момент времени и известной амплитуды колебаний:

х(0) = х₀ = А·cos f₀;    cos f₀ = х₀/A.

Следовательно, f₀ зависит от выбора начала отсчета времени. 

Например, если для колебаний, описываемых уравнением (9.1),  x(0) = х₀ = 0, то f₀ = p/2, если 
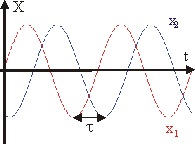
x(0) = х₀ = А, то f₀ = 0.

В случае, если амплитуда колебаний не известна, то для нахождения начальной фазы и амплитуды колебаний кроме начального смещения необходимо знать начальное значение скорости колеблющегося тела. 

Большое значение для анализа сложного колебательного движения имеет понятие разности фаз двух колебаний: DФ = Ф₂ - Ф₁. Если колебания синхронные (т.е  имеют одинаковую частоту), то величина DФ не зависит от времени и они происходят с постоянным сдвигом фаз. Пример такого рода колебаний приведен на рис. 9.3. Колебание величины x₁ = A₁·sin(w·t)  опережает колебание x₂ = A₂·sin(w·(t - t)).

Если колебания несинхронные, то величина DФ зависит от времени.

Синхронными называются гармонические колебания, имеющие одинаковые частоты.

Сдвиг фаз можно выразить в радианах и в долях периода. Пусть колебания подчиняются уравнениям:

x₁ = A₁·sin(2p·t/T);
x₂ = A₂·sin(2p·(t - t)/T),
где t - время запаздывания 2-го колебания относительно 1-го.

Второе колебание можно представить в следующем виде:

x₂ = A₂·sin(2p·t/T - 2p·t/T).

Очевидно, f₁ - f₂ = 2p·t/Т.     (9.2)

Из уравнения (9.2) следует, что если t = Т/4, то f₁ - f₂ = p/2, а при t = Т/2, сдвиг фаз f₁ - f₂ = p.

Рис. 9.4.

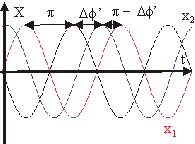
Колебания, происходящие со сдвигом фаз p, называются антифазными. Имеется некоторая неопределенность в отставании и опережении на p. Нельзя сказать, которое из колебание отстает, т. к. математически эти утверждения эквивалентны. Рассмотрим случай, когда х₂ отстает от х₁ больше, чем на p (см. рис. 9.4). Сдвиг по фазе Ф₁ - Ф₂ = p + Df' характеризует отставание 2-го колебания от 1-го. Из графика видно, что такое отставание эквивалентно опережению 2-м колебанием 1-го на угол Ф₂ - Ф₁ = p - Df'. Такой же результат получим и математически, исходя из тригонометрического равенства:

sin(p + Df) = sin(p - Df).

Чтобы не было этой неопределенности, условились сдвиг фаз задавать в диапазоне от 0 до p. 

Влияние параметров колебаний на их вид вы можете наблюдать на графиках, которые построите самостоятельно.

Кинематические характеристики гармонических колебаний. Найдем скорость и ускорение при колебательном движении, описываемого уравнением:

x = A·cos(w·t + f₀).

Поскольку скорость u - есть производная от координаты по времени, а ускорение a - соответствующая производная от скорости, то эти величины зависят от времени также по гармоническим законам:

u = A·w·cos(w·t + f₀);
a = - A·w²·sin(w·t + f₀) = - w²·x.     (9.3)

Выполнение соотношения (9.3) является характерным признаком гармонического колебательного движения. Для такого движения скорость опережает по фазе смещение на p/2, а ускорение - на p.

Рис. 9.5.

Представление гармонических колебаний с помощью метода векторных диаграмм. В ряде случаев оказывается полезным представить колебания скалярных величин с помощью векторов. Данный способ называется методом векторных диаграмм. 

В чем сущность этого метода? Для представления величины x, изменяющейся по гармоническому закону x = A·cos(w·t + f₀), изобразим на произвольной оси X вектор r, исходящим из точки O (см. рис. 9.5). Пусть длина данного вектора равна амплитуде A, а угол с осью X равен фазе Ф. 

Допустим, что вектор r вращается вокруг точки O с угловой скоростью w против часовой стрелки, что соответствует положительному направлению отсчета углов. Тогда угол между вектором и осью, равный фазе колебаний, будет изменяться по закону Ф(t) = w·t + f₀. Значение физической величины x в любой момент времени зададим как проекцию вектора r на ось Х:

r_x = x = A·cos(w·t + f₀).

Итак, скалярное гармоническое колебание можно представить как проекцию вектора с амплитудой A, который вращается вокруг закрепленной точки O с постоянной угловой скоростью w.

Сложение скалярных колебаний.

Рис. 9.6.

Сложение синхронных скалярных колебаний. Колебания векторных величин называются векторными, а скалярных величин - скалярными.

Примеры. Векторные колебания: колебания радиус-вектора частицы, напряженности электрического и магнитного полей (r, E, H); скалярные колебания: колебания давления, температуры (Р, T).

При сложении векторных колебаний нужно учитывать их направления, в то время как скалярные колебания складываются алгебраически. Рассмотрим сложение скалярных колебаний или векторных колебаний, направленных вдоль одной прямой.

Пусть мы имеем два синхронных скалярных колебания, описываемых законами:

x₁ = A₁·cos(w·t + f₁);
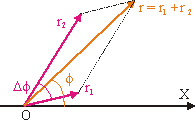
x₂ = A₂·cos(w·t + f₂).

Задача - найти результирующее колебание х = x₁ + x₂. Решение этой задачи значительно упрощается, если воспользоваться методом векторных диаграмм. Изобразим скалярные величины x₁ и x₂ в момент t = 0 в виде проекций векторов r₁ и r₂, вращающихся вокруг точки O с угловой скоростью w (см. рис. 9.6). 

Поскольку сумма проекций векторов r₁ и r₂, имеющих амплитуды A₁ и A₂, на ось X равна проекции на эту же ось результирующего вектора r = r₁ + r₂, то для получения искомого результата сначала по правилу сложения векторов (см. рис. 9.6) найдем вектор r, а затем вычислим его проекцию. 

Поскольку колебания синхронные, то взаимная ориентация векторов r₁ и r₂ с течением времени не изменится. Вектор r будет вращаться вокруг точки O со скоростью w и результирующее колебание будет гармоническим. В произвольный момент времени:

x =  A·cos (w·t + f).

Проекция x задается значениями амплитуды A и угла f: 

A² = A₁² + A₂² + 2A₁·A₂·cos(Df);     (9.4)
tg f = (A₁·sin f₁ + A₂·sin f₂)/(A₁·cos f₁ + A₂·cos f₂); (9.5)
x₀ =  A·cos f.

Из уравнений (9.4) и (9.5) следует, что амплитуда результирующего колебания зависит не только от соотношения амплитуд исходных колебаний, но и от сдвига фаз между ними Df = f₂ - f₁. 

Например, если f₂ = f₁, то A = A₁ + A₂, 
если f₂ - f₁ = p, то A = A₁ - A₂ (при A₁ = A₂ амплитуда результирующего колебания А = 0).

Рис. 9.7.

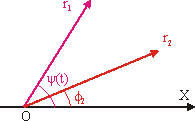
Биения. Пусть частоты двух скалярных колебаний не равны друг другу и w₁ > w₂. Сначала рассмотрим случай, когда разность частот складываемых колебаний мала, т.е. w₁ - w₂ = W << w₁, w₂.

x₁ =  A₁·cos (w₁·t + f₁);
x₂ =  A₂·cos (w₂·t + f₂).

Найдем результирующее колебание x = x₁ + x₂. Заменив величину w₁ на w₂ + W, запишем уравнение 1-го колебания в виде:

x₁ =  A₁·cos (w₂·t + (W·t+ f₁)) =
= A₁·cos (w₂·t + y(t)).

Величину y(t) будем рассматривать как медленно изменяющуюся во времени фазу y(t) = W·t+ f₁. Таким образом, вектор r₁ участвует в двух вращениях с частотами w₂ и W. Изобразим r₁ и r₂ на векторной диаграмме, исходящими из одной точки O. Не будем рассматривать их синхронного вращения с частотой w₂, т.к. оно не изменяет со временем их взаимного расположения этих векторов (см. рис. 9.7). Поэтому вектор r₂ будем считать  неподвижным, а r₁ - вращающимся со скоростью W относительно точки O. При вращении r₂ вектор r₁ составляет с ним некоторый угол, изменяющийся со временем. В результате сложения r₁ и r₂ получим вектор, длина которого периодически меняется со временем от значения, равного сумме A₁ + A₂, до значения, равного разности A₁ - A₂. Действительно, из (9.4) следует, что:

A² = A₁² + A₂² + 2A₁·A₂·cos(W·t + Df),    (9.6)
где Dj = f₁ - f_2.

Из (9.6) видно, что амплитуда результирующего колебания А изменяется по гармоническому закону с частотой W. Период изменения амплитуды равен Т_б = 2p/W. 

Рис. 9.8. Биения.

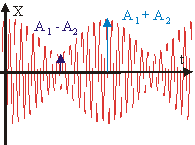
Периодическое изменение амплитуды результирующего колебания, являющегося результатом сложения скалярных гармонических колебаний с близкими частотами, называется биением. 

График биения будет иметь вид, представленный на рис. 9. 8. Видно, что результирующее колебание не является гармоническим.

Пример. Если два камертона заставить звучать с близкими частотами, то в результате сложения колебаний громкость звука, обусловленная амплитудой суммарного колебания, периодически меняется с частотой биений. Высота же звука существенно не меняется, т.к. она определяется частотой результирующего колебания, которая близка к частотам складываемых колебаний. Метод биений является чувствительным методом обнаружения разницы частот.

Сложение колебаний с кратными частотами. Если складываемые колебания имеют резко отличающиеся частоты, то результирующее колебание даже приблизительно не будет гармоническим. В случае, если частоты складываемых колебаний кратны, т.е. w₁/w₂ = n₁/n₂ (n₁ и n₂ - целые числа), то результирующее колебание не является гармоническим, но будет периодическим. Период колебания равен наименьшему кратному периодов исходных колебаний. 

Например, если Т₁ = 2 с, Т₁ = 3 с, то Т = 6 с.

Сложение векторных колебаний.

Рис. 9.9. Сложение синхронных взаимно перпендикулярных колебаний.

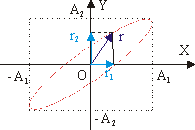
Сложение ортогональных колебаний с равными частотами. Рассмотрим два векторных колебания, описываемых уравнениями:

r₁ = A₁·cos(w₁·t + f₁);
r₂ = A₂·cos(w₂·t + f₂).

Заметим, что с течением времени направление векторов не изменяется, а изменяется только их амплитуда. Очевидно также, что вектор A₁ параллелен r₁, а вектор A₂ параллелен r₂. Задача: найти r = r₁ + r₂. Рассмотрим только случай взаимно-перпендикулярных колебаний.

Вдоль вектора r₁ направим ось Х, вдоль r₂ - ось Y. Очевидно, результирующий вектор r перемещается в плоскости XY. Кривая, описываемая концом вектора r, называется фигурой Лиссажу. Эта фигура вписывается в четырехугольник со сторонами 2·A₁ и 2·A₂, а ее вид зависит от соотношения частот, фаз и амплитуд складываемых колебаний. 

Рассмотрим случай синхронных взаимно-перпендикулярных колебаний (см. рис. 9.9):

r₁ = A₁·cos (w·t + f₁);     (9.7)
r₂ = A₂·cos (w·t + f₂).     (9.8)

Спроецировав уравнения (9.7) и (9.8) на оси координат и проведя суммирование проекций, получим:

x = A₁·cos (w·t + f₁);     (9.9)
y = A₂·cos (w·t + f₂).     (9.10)

Исключив с помощью тригонометрических преобразований t из (9.9) и (9.10), получим математическое выражение фигуры Лиссажу, которое представляет собой уравнение эллипса:

. (9.11)

Вид эллипса определяется величиной сдвига фаз Df. В общем случае, когда Df отлична от 0, полуоси эллипса повернуты относительно осей X и Y на определенный угол.

Если сдвиг фаз Df = 0, то как следует из уравнения (9.11) будет справедливо следующее выражение:

(х/А₁ - y/A₂)² = 0 или
y = А₂·x/А₁.

Т.е. фигура Лиссажу представляет из себя прямую линию с углом наклона a к оси X (tg a = А₂/А₁). Если Df = p, то y = - А₂·x/А₁.

Если Df = p/2, то имеем классическое уравнение эллипса, полуоси которого параллельны осям координат:

х²/А₁² + y²/A₂² = 1.

Если Df = p/2 и А₁ = А₂ = A, то эллипс превращается в окружность радиуса A.

Рис. 9.10.

Рис. 9.11.

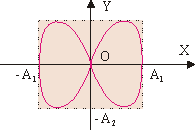
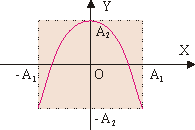
Сложение ортогональных колебаний с кратными частотами. Рассмотрим случай сложения несинхронных перпендикулярных колебаний. Пусть w₁ не равняется w₂, но частоты исходных колебаний относятся как целые числа: w₁/w₂ = n₁/n₂. Рассмотрим следующий пример:

x = A₁·sin w·t;
y = A₂·sin (2·w·t). 

Для нахождения вида фигуры Лиссажу используем метод графического исключения t. Изобразим на одном графике зависимости x(t) и y(t). Отметим на этом графике положение точек в некоторые последовательные моменты времени. Затем перенесем эти точки на плоскость XY. В результате получим фигуру Лиссажу типа восьмерки (см. рис. 9.10). Если взять колебания с разными начальными фазами, то при таком же соотношении частот также получим фигуры Лиссажу типа восьмерки, но не симметричные относительно осей координат. При Df = p/2, фигура Лиссажу примет вид параболы (см. рис. 9.11).

Существует правило частот Лиссажу, по которому можно определить частоты складываемых колебаний. Об их соотношении судят по числу точек пересечения фигуры прямыми, параллельными осям координат:

w_y/w_x = n_x/n_y.

Откуда это следует? Обозначим за t - минимальное время, в течение которого полностью описывается фигура Лиссажу. Очевидно, что t равно наименьшему кратному периодов колебаний T_x и T_y, совершающихся вдоль осей X и Y. За один период конец вектора r пересечет ось X 2 раза. Следовательно, за время t число пересечений этой оси будет равно n_x = 2·t/T_y. Аналогично n_y = 2·t/T_x. Следовательно, n_y/n_x  = T_y/T_x = w_x/w_y.

Метод фигур Лиссажу широко используется для определения соотношения частот и фаз складываемых колебаний (например, в радиотехнике для градуировки генераторов). Чувствительность фигуры Лиссажу к разности фаз используется также для исследования фазовых соотношений в цепях переменного тока.

Энергия собственных колебаний.

Механическая энергия незатухающих колебаний. Рассмотрим груз на пружине, совершающий гармонические колебания. 

Система, совершающая гармонические колебания называется гармоническим осциллятором. 

Так как F_тр = 0, то система "груз + пружина" является замкнутой и консервативной, то ее полная механическая энергия, равная сумме кинетической и потенциальной энергий, не изменяется:

E = Е_к + Е_п = const.

Подсчитаем полную механическую энергию Е гармонического осциллятора, совершающего колебания по закону x = A·sin(w₀·t + f₀). При выводе учтем, что k = w₀²· m.

Е_к = m·u²/2 = m·A²·w₀²/2·cos²(w₀·t + f₀);
Е_п = k·x²/2 = m·A²·w₀²/2·sin²(w₀·t + f₀).

Следовательно,

E = m·A²·w₀².     (9.12)

Энергия гармонического незатухающего осциллятора пропорциональна квадрату амплитуды и собственной частоты и пропорциональна его массе.

Отредактировано 22.04.2001

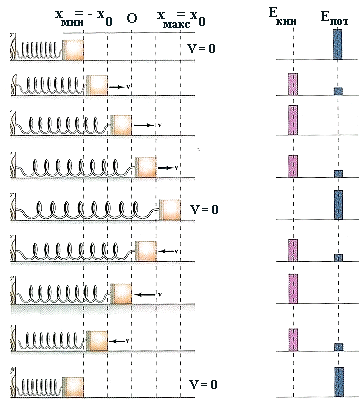
Механическая энергия собственных затухающих колебаний. Из закона сохранения энергии следует, что по мере совершения колебаний кинетическая энергия переходит в потенциальную и наоборот (см. рис. 9.12).

Рис. 9.12.

Максимальные значения кинетической и потенциальной энергий равняются максимальному значению полной механической энергии. При наличии трения в системе полная механическая энергия системы с течением времени уменьшается, но ее мгновенное значение, по-прежнему, равняется максимальной потенциальной энергии, относящейся к данному моменту времени. Следовательно, для затухающих колебаний, подчиняющихся закону (см. лекцию 10)
x = A₀·e^{- d·t}·sin(w₀·t + f₀), будет справедливо выражение:

E(t) = Е_п.макс = k·A(t)²/2 = m·A₀²·w₀²·e^{- 2·d·t}/2.

Аналогичное выражение можно получить, рассчитав максимальное значение кинетической энергии (см. решение задач по теме "Колебания", занятие 2).
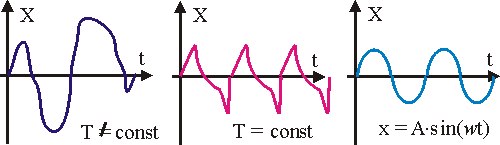
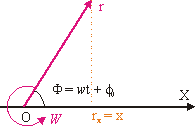