Общие понятия теории собственных колебаний.

Собственными называются колебания, которые совершает система около положения устойчивого равновесия после первоначального возмущения под действием только внутренних сил.

Какая сила должна действовать на систему, чтобы колебания были гармоническими? Так как для гармонических колебаний уравнение, связывающее ускорение и координату материальной точки выглядят как

а = - w²·х, 

то согласно II закону Ньютона справедливо следующее равенство:

F = m·a = - m·w²·х = - k·x,      (10.1)
где k - постоянная величина.

Итак, тело совершает гармонические колебания, если сила, возвращающая его в положение равновесия, пропорциональна смещению и направлена в противоположную этому смещению сторону. 
Такая сила называется квазиупругой.

На практике зависимость F(x) является более сложной. Однако, при малых значениях величины х эту функцию можно разложить в ряд:

|F(x)| = k·x + k₁·x² + k₂·x³ + ...

и пренебречь слагаемыми более высокого, чем 1 порядка малости. Следовательно, любая система с одной степенью свободы при достаточно малом отклонении от положения равновесия будет гармонически колебаться.

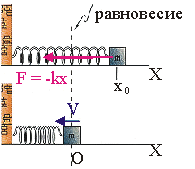
Рис. 10.1.

Уравнение динамики собственных колебаний. Рассмотрим колебания груза на пружине, считая, что вся масса сосредоточена в грузе, а упругость - в пружине. При х = 0 пружина не деформирована (см. рис. 10.1). Предположим, что сила трения в системе отсутствует F_тр = 0. В случае смещения тела от положения равновесия возникает сила упругости, действующая на тело и стремящаяся возвратить его в положение равновесия. Поскольку при малых деформациях х эта сила равна F = - k·x, то уравнение динамики движения груза согласно II закону Ньютона можно записать в виде:

m·a = - k·x.      (10.2)

Поскольку ускорение - есть вторая производная от координаты по времени, то решив дифференциальное уравнение (10.2), найдем зависимость x(t). В теории дифференциальных уравнений показано, что общим решением уравнений типа x'' + w₀²·x = 0 выражается зависимостью вида: x = A·cos(w₀·t + f₀). 

Можно рассуждать также следующим образом. Из (10.2) имеем, что для гармонических колебаний a = - w₀²·x, т.е. ускорение а пропорционально х и направлено в противоположную к нему сторону. Следовательно, колебания груза в случае выполнения условия (10.2) являются гармоническими и описываются уравнением:

x = A·cos(w₀·t + f₀),    (10.3)
где w₀ = (k/m)^1/2 - собственная частота колебаний.

Значение w₀ зависит только от физических свойств системы и не зависит от начальных условий.

Расчет параметров собственных колебаний. Амплитуда A и начальная фаза f₀, называемые параметрами колебаний, не зависят от свойств системы, а определяются только начальными условиями, т.е. значением смещения и скорости в начальный момент времени:

x(0) = x₀;      u(0) = u₀.

Задав x₀ и u₀, получим два уравнения для расчета амплитуды и начальной фазы:

x₀ = A·sin f₀;            (10.4)
u₀ = A·w₀·cos f₀.     (10.5)

Уравнения (10.4) и (10.5) задают значения A и f₀.

A = (x₀² + u₀²/w₀²)^1/2;
tg f₀ = x₀·w₀/u₀.

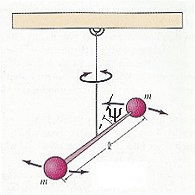
Рис. 10.2. Крутильные колебания.

Примеры собственных колебаний.
Крутильные колебания (см. рис. 10.2). Пусть y - угловая координата, I - момент инерции, K - модуль кручения. Уравнение динамики крутильных колебаний имеет вид:

I·e = - K·y или
y'' = - K·y/I.     (10.6)

Сравнивая уравнения (10.6) и (10.1), видим, что они аналогичны. Следовательно, решение уравнения (10.6) имеет вид гармонической функции:

y(t) = y_max·sin((K/I)^1/2·t + f₀).

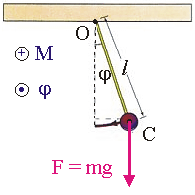
Рис. 10.3. Колебания физического маятника.

Физический маятник (см. рис. 10.3). Физическим маятником называется система, способная совершать колебания около положения равновесия, при этом массу системы нельзя считать сосредоточенной в одной точке. Введем обозначения: O - точка вращения; С - положение центра масс маятника; l - его длина; j - угол отклонения от положения равновесия. Уравнение динамики вращательного движения для физического маятника в проекции на ось вращения в случае его малых колебаний запишем в виде:

M_z = I·j'' = - m·g·l·sin j = - m·g·l·j.

Решение этого уравнения имеет следующий вид:

j(t) = j_max·sin(w₀·t + f₀),
где w₀ = (m·g·l/I)^1/2.

Для математического маятника момент инерции и значение собственной частоты колебаний будут равны: 

I = m·l² и 
w₀ = (g/l)^1/2.

Собственную частоту физического маятника можно представить в виде, аналогичном выражению для математического маятника:

w₀ = (g/l_прив)^1/2, 
где l_прив = I/(m·l) - приведенная длина маятника.

Собственные затухающие колебания. Логарифмический декремент затухания.

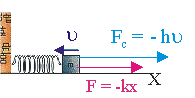
Рис. 10.4.

Уравнение динамики затухающих колебаний. В реальных случаях на тело, совершающее собственные гармонические колебания, действует сила трения. Наиболее распространен случай жидкого трения, когда сила трения (сопротивления среды) пропорциональна скорости:

F_тр = - h·u,      (10.7)
где h - коэффициент сопротивления среды. 

Уравнение (10.7) справедливо для малых скоростей. Согласно II закону Ньютона уравнение движения тела будет иметь вид:

m·x'' = - k·x - h·x'.

После несложных преобразований получим:

x'' + h/m·x' + k/m·x = 0;
x'' + 2·d·x' + w₀²·x = 0.     (10.8)

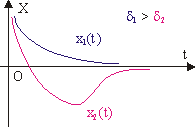
Рис. 10.6. Затухающие колебания в случае большого трения.

Решение уравнения динамики для случая большого и малого трения. Решение дифференциального уравнения (10.8) будет разным по характеру в зависимости от величины коэффициента сопротивления. При w₀² > d², т.е. в случае малого сопротивления среды, тело совершает колебательное движение, а решение имеет вид:

x(t) = A₀·e^-d·t·sin(w·t + j₀).     (10.9)

Величины A₀ и j₀, по-прежнему, определяются начальными условиями, а циклическая частота затухающих колебаний равна

w = (w₀² - d²)^1/2     (10.10)

и определяется характеристиками колеблющейся системы и окружающей среды. Таким образом, трение уменьшает частоту колебаний. Качественно этот факт можно объяснить так. Сила трения действует против скорости. Следовательно, для линейного осциллятора ее действие эквивалентно уменьшению возвращающей силы, т.е. упругости пружины. Это означает, что частота колебаний w уменьшается, а период Т увеличивается.

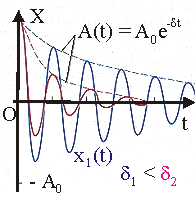
Рис. 10.5. Затухающие колебания.

График затухающего колебания представляет собой амплитудно-модулированную синусоиду (см. рис. 10.5). Модулирующая функция - экспонента равна:

 А(t)  = A₀·e^-d·t.     (10.11)

Колебание в данном случае не является гармоническим и даже периодическим. Условно, периодом затухающего колебания называется минимальный промежуток времени между локальными максимумами или минимумами функции x(t). 

При большом трении тело колебаний как таковых не совершает (см. рис. 10.6, кривая x₁(t)). Решение будет иметь вид:

x(t) = A₀·e^{-(d + (d2 - w02)1/2)·t}.

Возможен и промежуточный вариант, также характерный для больших значений коэффициента затухания (кривая x₂(t) на рис. 10.6).

Коэффициент затухания. Коэффициент d, определяющий быстроту изменения амплитуды, называется коэффициентом затухания. Если промежуток времени Dt = 1/d, то А₀/А = е. Отсюда вытекает физический смысл коэффициента затухания: 

величина 1/d, равна промежутку времени, по истечении которого амплитуда колебаний уменьшается в е = 2.73 раз.

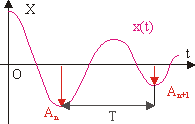
Рис. 10.7. К определению логарифмического декремента затухания.

Логарифмический декремент затухания, добротность. Коэффициент затухания d не дает полного представления об интенсивности затухания. Допустим, что для одного осциллятора колебания прекратились через 10 секунд, а для второго - через 100. Какой из осцилляторов обладает более быстрым затуханием? На этот вопрос ответить невозможно, если не учесть, сколько колебаний система успела совершить за это время. 

Для характеристики интенсивности затухания вводят понятие логарифмического декремента затухания. Пусть Т - условный период затухающего колебания, А_n и A_n+1 - амплитудные значения функции x(t) для двух ее последовательных экстремумов (см. рис. 10.7). Величина d, равная:

d = ln(А_n /A_n+1)     (10.12)

называется логарифмическим декрементом затухания. Выясним связь между d и d:

d = ln( А_n /A_n+1) = ln(A₀·e ^{- d·t}/A₀·e ^{- d·(T + t)}) = 
= ln(e ^d·T) = d·T = d.     (10.13)

Используя уравнение (10.13), можно преобразовать закон изменения амплитуды:

A_n = A₀·e^-d·t = A₀·e^-d·T·t/T = A₀·e^-d·n,     (10.14)
где n = t/T - число колебаний за время t.

A_n = A₀·e^-d·n.

Если n = 1/d, то A₀/A_n = e. 

Величина 1/d равна числу колебаний, за которое их амплитуда уменьшается в е раз.

Если значение d невелико (d << 1), то можно показать, что

(A_n - A_n+1)/A_n = d.     (10.15)

Логарифмический декремент связан с другой важной характеристикой колебаний - добротностью q следующим соотношением:

q = p/d.     (10.16)

Динамика вынужденных колебаний. Резонанс.

Уравнение динамики колебаний, происходящих  под действием гармонической силы. Вынужденными называются колебания, которые система совершает под действием внешней силы. Характер движения зависит от особенностей внешней силы. Она может быть любой периодически изменяющей свое значение. Наиболее важным является случай гармонической внешней силы. Более сложные случаи ее изменения во времени сводятся к этому простейшему.

Будем считать, что внешняя сила действует на линейный гармонический осциллятор по следующему закону:

F = F₀·cos(w·t).

Кроме внешней силы на осциллятор, по-прежнему, действуют квазиупругая сила и сила трения. Согласно II закону Ньютона уравнение движения имеет вид:

m·x'' + h·x' + k·x = F₀· cos(w·t)
или
x'' + 2·d·x' + w₀²·x = F₀· cos(w·t)/m.     (10.17)

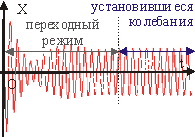
Рис. 10.8.

Уравнение вынужденных колебаний. Уравнение (10.17) - линейное неоднородное дифференциальное уравнение II порядка. В неоднородном уравнении, в отличии от однородного, существуют слагаемые, содержащие аргумент (в нашем случае переменную t).

Решение неоднородного уравнения x(t) представляет сумму общего решения однородного уравнения x₁(t) и частного решения неоднородного уравнения x₂(t), т.е. x(t) = x₁(t) + x₂(t). Первое нам известно - это решение уравнения собственных затухающих колебаний, а второе, исходя из тригонометрических соображений, будем искать в виде:

х₂(t) = A·cos(w·t + f),
где A и f - постоянные величины, представляющие собой амплитуду и сдвиг фаз между смещением и внешней силой.

Таким образом, общее решение будут иметь вид:

x(t) = A₀·e^-d·t·sin(w·t + j₀) + A·cos(w·t + f).     (10.18)

Первое слагаемое правой части этого выражения описывает собственные затухающие колебания, зависящие от начальных условий. Из уравнения (10.18) следует, что в течение определенного промежутка времени осциллятор будет совершать сложное негармоническое движение, т.к. оно является результатом сложения двух асинхронных колебаний. Однако, через промежуток времени t ~ 1/d амплитуда и энергия собственных колебаний уменьшатся до нуля и они прекратятся. При этом второе слагаемое останется неизменным и результирующее колебание будет гармоническим (см. рис. 10.8, 10.9).

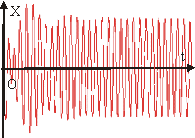
Рис. 10.9.

Переходной и установившийся режимы колебаний. Колебания, которые будут совершаться после затухания собственных колебаний, называются установившимися вынужденными колебаниями. Процесс установления этих колебаний называется переходным режимом (см. рис. 10.8). 

Установившиеся колебания не зависят от начальных условий и описываются уравнением: 

х = A·cos(w·t + f).     (10.19)

Частота вынужденных колебаний w равна частоте вынуждающей силы, а амплитуда A и сдвиг фаз f смещения относительно внешней силы зависят от значений собственной частоты колебаний w₀, частоты вынуждающей силы w и коэффициента затухания d (см. рис. 10.8, 10.9).

Параметры вынужденных колебаний. Найдем величины А и f. Для этого подставим уравнение (10.19) и его производные по времени в выражение (10.17). Воспользовавшись методом векторных диаграмм, получим, что уравнение обращается в тождество только для определенных значений A и f.

A = (F₀/m)/((w₀² - w²)² + 4d²·w²)^1/2.    (10.20)

Амплитуда вынужденных колебаний пропорциональна амплитуде вынуждающей силы и существенно зависит от соотношения между частотой вынуждающей силы и собственной частотой.

Величину сдвига фаз между смещением и вынуждающей силой будет равна:

tg f = - 2d·w/(w₀² - w²).     (10.21)

Обратите внимание, что смещение отстает по фазе от вынуждающей силы.

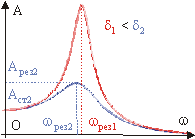
Рис. 10.10. Амплитудно-резонансная кривая.

Амплитудная резонансная кривая. Резонанс. Построим зависимость А(w), график которой называется амплитудной резонансной кривой. Вид этой кривой зависит от величины коэффициента затухания d (см. рис. 10.10). Амплитуда, соответствующая значению частоты w = 0, называется статическим смещением. Т.к. F₀ = k·A_ст, то

А_ст = F₀/(m·w₀²) = F₀/k.     (10.21)

Из графика видно, что при определенном значении частоты вынуждающей силы амплитуда осциллятора становится максимальной.

Явление, при котором  амплитуда колебаний системы достигает максимального значения, характерного для некоторого значении частоты вынуждающей силы называется резонансом. 

Частота вынуждающей силы, при которой наступает данное явление, называется резонансной. Приравнивая к нулю производную по частоте выражения (10.20) и пренебрегая слагаемыми второго порядка малости, получим формулы для расчета резонансной частоты w_рез и амплитуды А_рез:

w_рез = (w₀² - 2d²)^1/2;     (10.22)
А_рез = F₀/(2m·d·w₀).      (10.23)

При значении d = 0 амплитуда колебаний в резонансе стремится к бесконечности. 

Важной характеристикой осциллятора является отношение амплитуды его колебаний в резонансе к ее статическому значению. Из формул (10.21) и (10.23) следует, что это отношение равно добротности системы:

А_рез/А_ст = p/d = Q,
где d - логарифмический декремент затухания.

Добротность является важнейшей характеристикой резонансных свойств системы.

Рассмотрим чему равен сдвиг фаз между смещением и силой при резонансе. Допустим, что при w = w₀ сила и смещение подчиняются следующим законам:

F = F₀·cos(w₀·t);
x = A·sin(w₀·t).

Тогда уравнение для скорости колеблющейся частицы (осциллятора) имеет вид:

x' = u = - A·w·cos(w₀·t).

Из этих соотношений видно, что скорость u и сила колеблются в фазе. Следовательно, мощность, сообщаемая осциллятору внешней силой, равна N = F·u. Ее значение положительно в любой момент времени, следовательно, работа внешней силы достигает своего максимального значения. Энергия, передаваемая осциллятору внешней силой, в этом случае направлена на преодоление сил трения.

Примеры. Явление резонанса используется в работе резонансных контуров в электрических схемах, усиливающих полезный сигнал, наличие резонанса необходимо учитывать при расчете механических конструкций на прочность.

Отредактировано: 22.04.2001